Multipack I

Title description

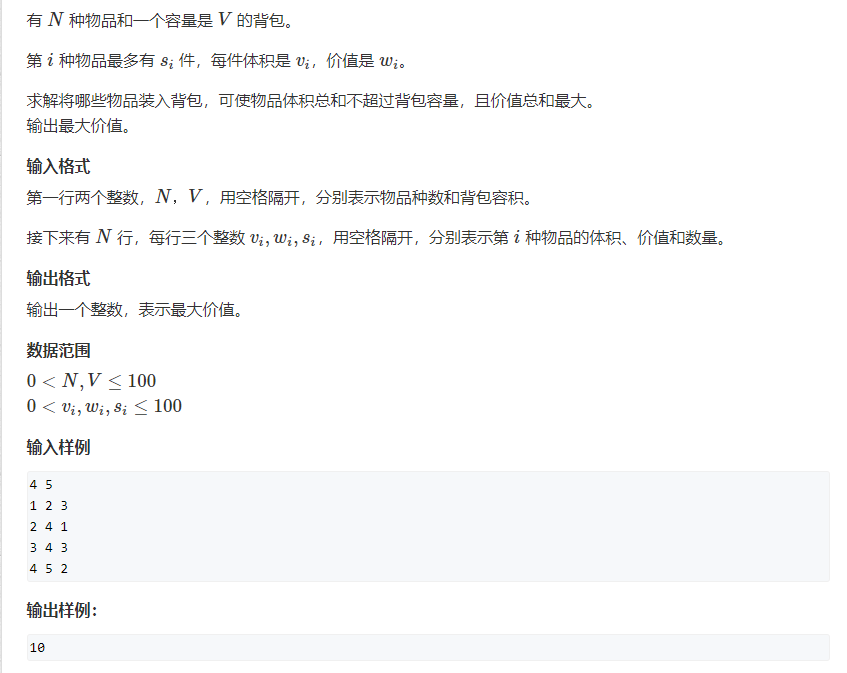
Plain version code (time complexity: O(NVS))

#include <iostream>

using namespace std;

const int N = 110;

int n,m;
int v[N],w[N],s[N];
int f[N][N];

int main()
{
    cin >> n >> m;
    
    for(int i=1;i<=n;i++) cin >> v[i] >> w[i] >> s[i];
    
    for(int i=1;i<=n;i++)
        for(int j=0;j<=m;j++)
            for(int k=0;k <=s[i] && k * v[i] <=j;k++) // Limit 1: Quantity, Limit 2: Volume
                f[i][j] = max(f[i][j],f[i-1][j-v[i] * k] + w[i] * k);
    
    cout<<f[n][m]<<endl;
    
    return 0;
}

Update while reading

#include <iostream>

using namespace std;

const int N = 110;

int n,m;
int f[N][N];

int main()
{
    cin >> n >> m;
    
    for(int i=1;i<=n;i++)
    {
        int v,w,s;
        cin >> v >> w >> s;
        
        for(int j=0;j<=m;j++)
            for(int k =0;k<=s && k * v <= j;k++)
                f[i][j] = max(f[i][j],f[i-1][j - k * v] + k * w);
    }
    
    cout<<f[n][m]<<endl;
   
    return 0;
}

Use rolling array to optimize one dimension

#include <iostream>

using namespace std;

const int N = 110;

int n,m;
int v[N],w[N],s[N];
int f[N];

int main()
{
    cin >> n >> m;
    
    for(int i=1;i<=n;i++) cin >> v[i] >> w[i] >> s[i];
    
    for(int i=1;i<=n;i++)
        for(int j=m;j>=0;j--)
            for(int k=0;k<=s[i] && k * v[i] <=j;k++)
                f[j] = max(f[j],f[j - k * v[i]] + k * w[i]);
    
    cout<<f[m]<<endl;
    
    return 0;
}

Multiple knapsack problem II (binary optimization, it can be seen that multiple knapsacks are also special 01 knapsacks)

Title description (note that the data range has been expanded to 1000)

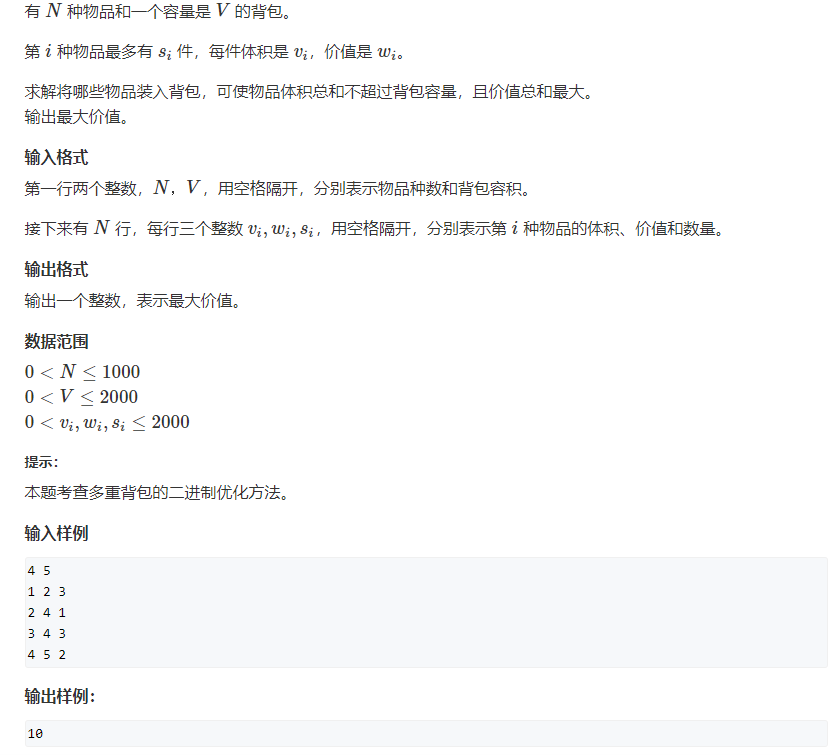
Code (time complexity: O(NVlog(S))

#include <iostream>

using namespace std;

const int N = 12010, M = 2010; // N = 2000 * log(2000)
// Core: Use binary to split s parts into log(s) parts

int n,m;
int v[N], w[N];
int f[M];

int main()
{
    cin >> n >> m;
    
    int cnt = 0;
    for(int i=1;i<=n;i++)
    {
        int a,b,s;
        cin >> a >> b >> s;
        int k = 1;
        while(k <= s)
        {
            cnt ++ ;
            v[cnt] = a * k;
            w[cnt] = b * k;
            s -= k;
            k *= 2;
        }
        if(s > 0) // The rest are put together
        {
            cnt ++ ;
            v[cnt] = a * s;
            w[cnt] = b * s;
        }
    }
    
    n = cnt; // There are a total of cnt groups, do the 01 backpack again
    
    for(int i=1;i<=n;i++)
        for(int j = m; j >= v[i]; j --)
            f[j] = max(f[j],f[j - v[i]] + w[i]);
    
    cout<<f[m]<<endl;
    
    return 0;
}

Concise version (update while reading, and scrolling array optimization)

#include <iostream>

using namespace std;

const int N = 12010, M = 2010; // N = 2000 * log(2000)
// Core: Use binary to split s parts into log(s) parts

int n,m;
int f[M];

int main()
{
    cin >> n >> m;
    
    for(int i=0;i<n;i++)
    {
        int v,w,s;
        cin >> v >> w >> s;
        
        for(int k = 1;k <= s;k *= 2)
        {
         	for(int j = m;j >= k * v; j -- )
             	f[j] = max(f[j], f[j - k * v] + k * w);
         	s -= k;
        }
        
        if(s)
        {
            for(int j = m;j >= s * v;j --)
                f[j] = max(f[j],f[j-s * v] + s * w);
        }
    }
    
    cout<<f[m]<<endl;
    
    return 0;
}

Multiple knapsack problem III

Title description (note the data range)

Monotonic queue optimization (time complexity: O(NV))

Code

#include <iostream>
#include <cstring>

using namespace std;

const int N = 20010;

int n,m;
int f[N],g[N],q[N];

int main()
{
    cin >> n >> m;
    for(int i=0;i<n;i++)
    {
        int v,w,s;
        cin >> v >> w >> s;
        memcpy(g,f,sizeof f);
        for(int j =0;j<v;j++)
        {
            int hh=0,tt=-1;
            for(int k =j;k<=m;k+=v)
            {
                if(hh <= tt && q[hh] < k - s * v) hh ++;
                if(hh <= tt) f[k] = max(f[k],g[q[hh]] + (k - q[hh]) / v * w);
                while(hh <= tt && g[q[tt]] - (q[tt] - j) / v * w <= g[k] - (k - j) / v * w) tt--;
                q[++ tt] = k;
            }
        }
    }
    
    cout<<f[m]<<endl;
    
    return 0;
}