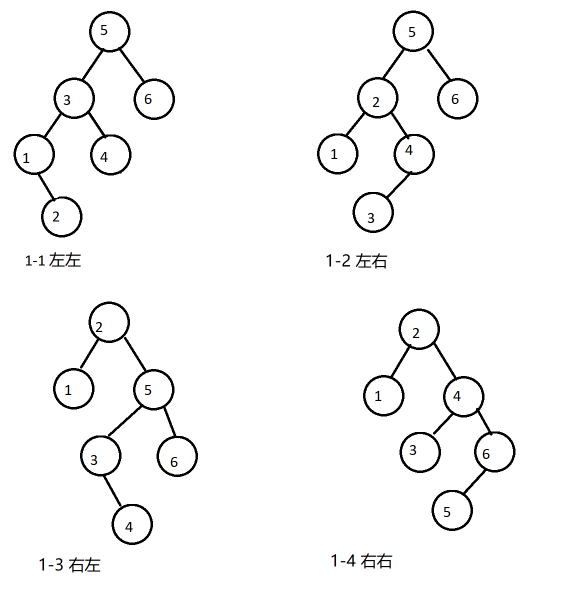
The rotation of the tree of the binary tree learning notes
Tree rotation is a subtree adjustment operation in a binary tree. Each rotation does not affect the result of the in-order traversal of the binary tree.
Tree rotation is often used where you need to adjust the local balance of the tree.
Left-handed and right-handed
The rotation of the tree has two basic operations, left-handed (counterclockwise rotation) and right-handed (clockwise rotation).

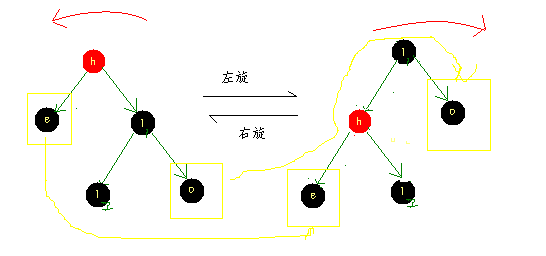
Tree rotation consists of two different ways, left rotation (with P as the axis of rotation) and right rotation (with Q as the axis of rotation). Both rotations are mirror images and are inverse to each other.
The following figure shows the initial and final states of the subtree during the two tree rotations.
+---+ +---+ | Q | | P | +---+ +---+ / \ right rotation / \ +---+ +---+ -------------> +---+ +---+ | P | | Z | | X | | Q | +---+ +---+ <------------- +---+ +---+ / \ left rotation / \ +---+ +---+ +---+ +---+ | X | | Y | | Y | | Z | +---+ +---+ +---+ +---+The detailed steps of the right rotation are as shown in the following three steps: R0, R1, and R2, and the left rotation is as shown in the three steps of L0, L1, and L2.
__ / \ +---+ / +---+ | Q | / | Q | +---+ +---+ +---+ / +---+ +---+ | P | / \ R1 | P |/ / \ +---+ | Q | R0 +---+ / +---+ -----> +---+ / +---+ R2 | P | +---+ -----> / \ / | Z | / / | Z | -----> +---+ / \ +---+ +---+ +---+ +---+ +---+ +---+ / \ +---+ +---+ | X | | Y | | X | | Y | +---+ +---+ | P | | Z | +---+ +---+ +---+ +---+ | X | | Q | +---+ +---+ __ +---+ +---+ / \ / \ / \ +---+ +---+ L2 +---+ \ +---+ L0 +---+ +---+ | X | | Y | <----- | P | \ | P | <----- | Y | | Z | +---+ +---+ +---+ \ +---+ L1 +---+ +---+ +---+ +---+ / \ \| Q | <----- / \ | Q | +---+ \ +---+ +---+ \ +---+ | X | \ \ | X | \ / \ +---+ +---+ +---+ +---+ +---+ +---+ | Y | | Z | | Y | | Z | +---+ +---+ +---+ +---+
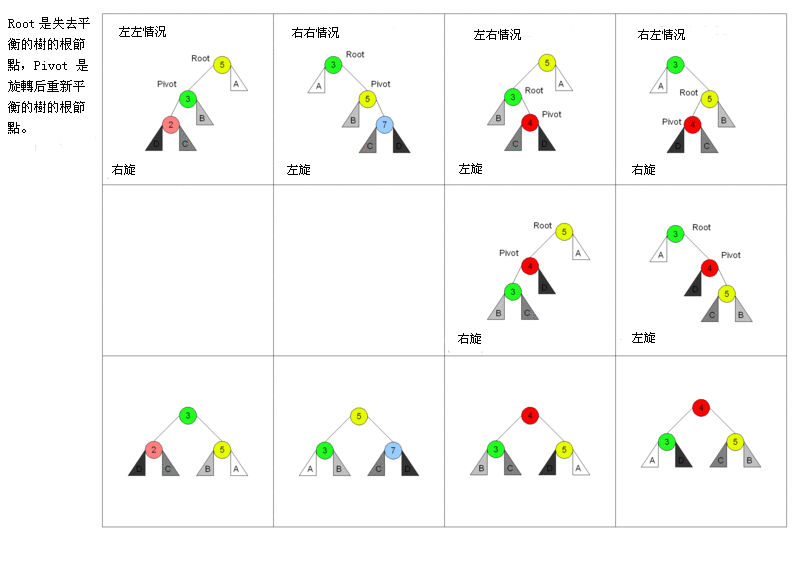
AVL tree adjustment
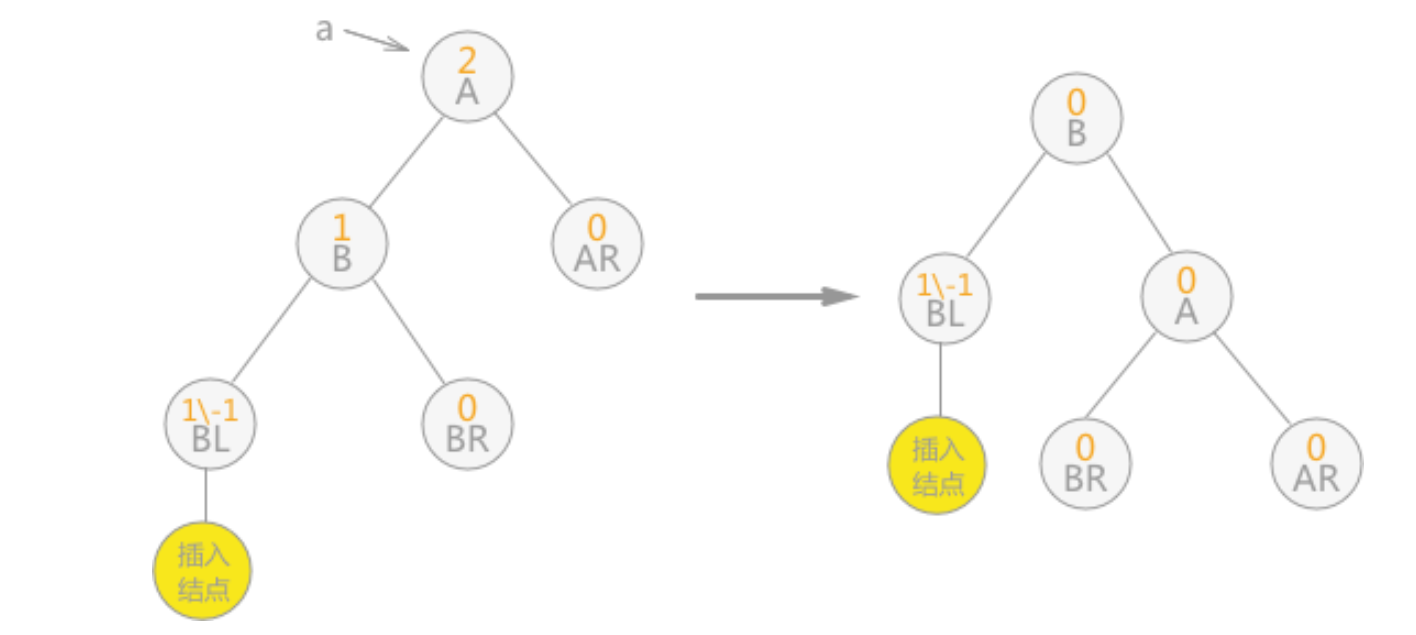
The basic operation of the AVL tree generally involves operating the same algorithm as the unbalanced binary search tree. But do the so-called "AVL rotation" one or more times in advance or later.
Intelligent Recommendation
Binary balance tree learning notes
The binary sorting tree increases the efficiency of finding, deleting, insertion, but if it is in order to insert: For example, the array {1, 2, 3, 4, 5, 6, 7, 8, 9} At this time The sort tree has bec...
Single rotation and double rotation of balance binary tree
Single rotation and double rotation of balance binary tree Balance the imbalance scenario after insertion of the binary tree When inserting new data into a balance binary tree, it can be found in the ...
Balanced binary tree insertion rotation
Balanced binary tree definition (AVL tree) The balanced binary tree is introduced on the binary sort tree (BST) to solve the imbalance of the binary sorting tree, and the imbalance is the main reason ...
Comprehension of balanced binary tree rotation
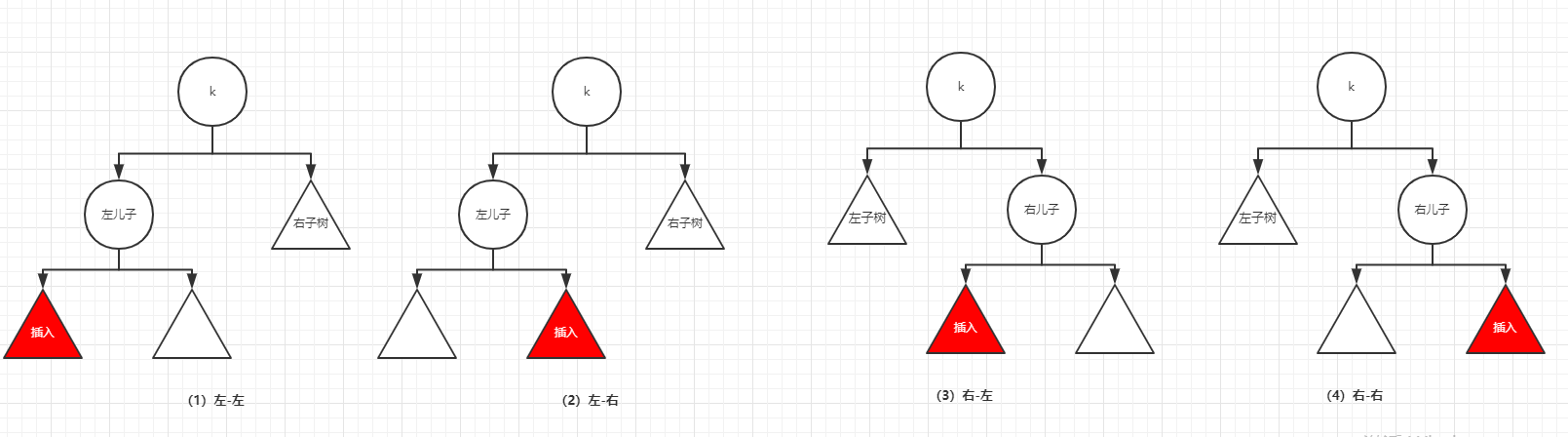
1. Left subtree left inserted -> right hand Inserting to the left of A’s left subtree causes A to be unbalanced Just look at BL, B, A, AR 4 points, turn right to become Then look at the BR no...
More Recommendation
Balance rotation of binary tree AVL
1. Introduction to the balanced binary tree AVL tree The AVL tree is the first self-balancing binary search tree (Self-Balancing Binary Search Tree, abbreviated as balanced binary tree). Definition of...
[Data Structure] Rotation of Binary Tree
In many balanced trees, tree rotation is used to maintain, such as red-black trees, and tree heaps (Treap) commonly used in competitions. The rotation of the tree must be able to change the maximum...
Notes - tree and binary tree
Binary tree recursive definition 1. either no root binary tree is empty tree 2. Either binary tree root node, the left subtree, right subtree composition, and the left and right subtree is the subtree...
Tree and binary tree notes
1. The basic concept of tree and binary tree Trees are a layered structure, which is used to organize data with branch -level relationships. 1.1 Basic concept of tree Node: The number of children of n...
Balance the rotation of AVL tree of binary tree
Balanced binary tree is a kind of self-balanced binary tree based on binary sorting tree (or also called binary search tree), such as AVL tree, red-black tree, etc. Definition of binary search tree (W...