1. Merge Sort

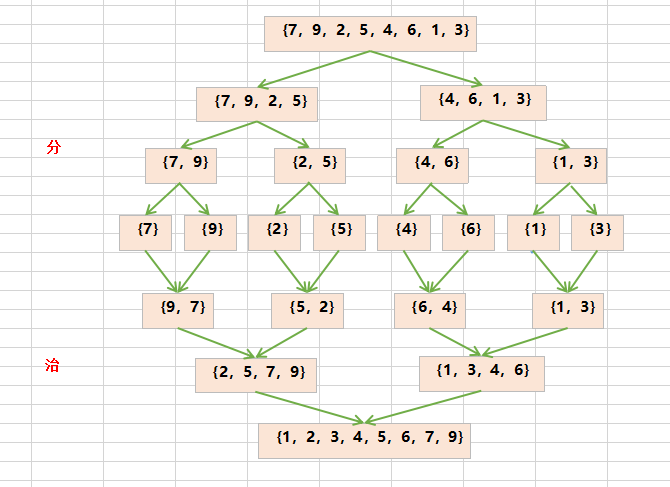
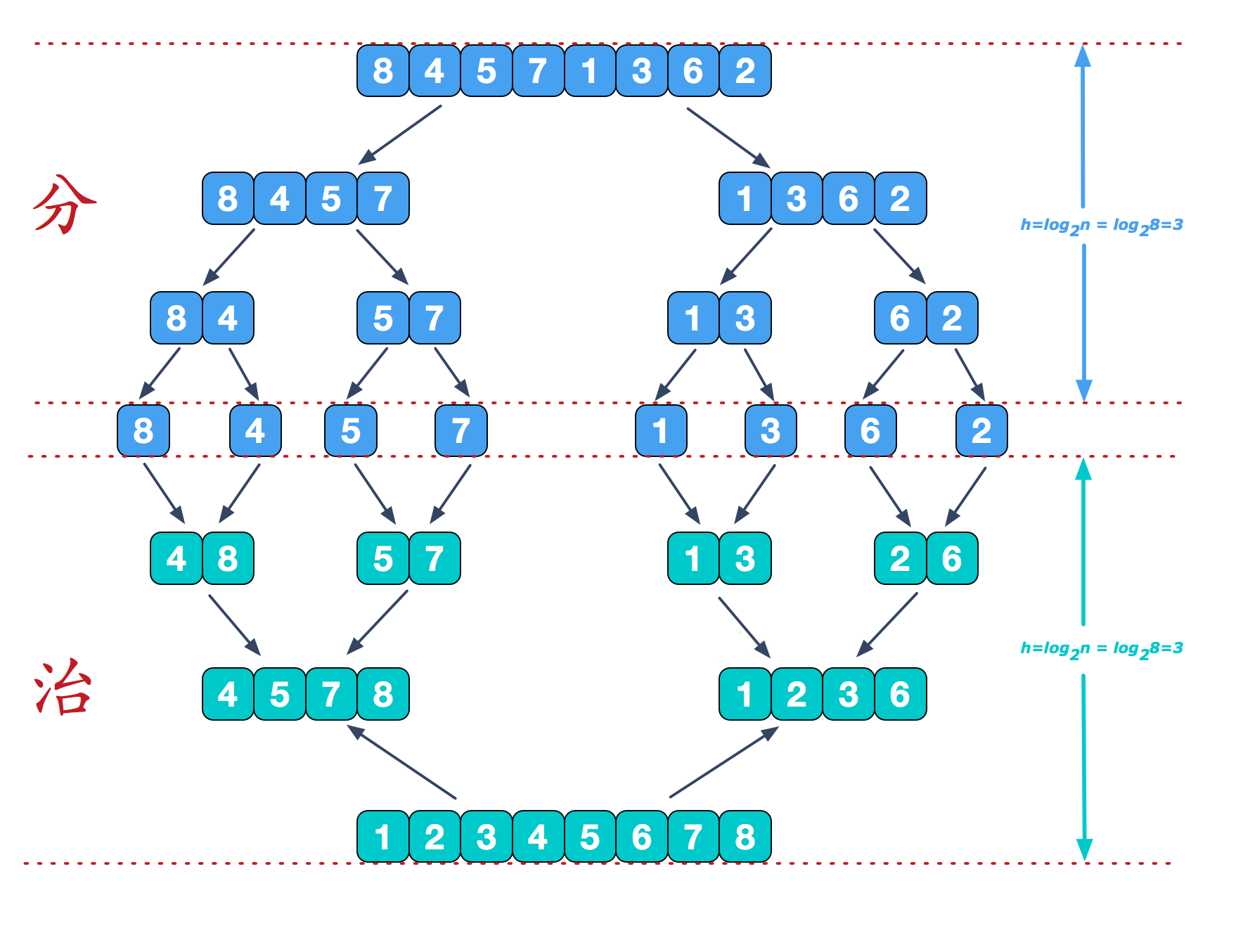
Merge sort is a very typical application of divide and conquer. The idea of ​​merge sort is to decompose the array recursively first, and then merge the array.
After decomposing the array to the smallest value, then merge the two ordered arrays. The basic idea is to compare the first number of the two arrays. Move one back. Then compare until one array is empty, and finally copy the remaining part of the other array.

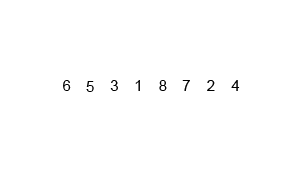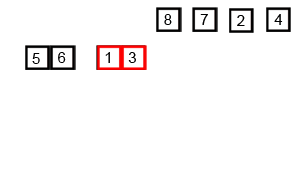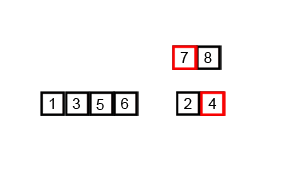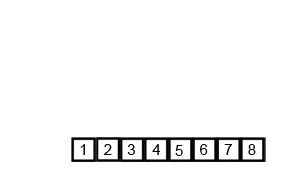
1.1 Implementation of merge sort

def merge_sort(alist):
    if len(alist) <= 1:
        return alist
    # Binary decomposition
    num = len(alist)/2
    left = merge_sort(alist[:num])
    right = merge_sort(alist[num:])
    # Merge
    return merge(left,right)

def merge(left, right):
    '''Merge operation, merge the two ordered arrays left[] and right[] into one big ordered array'''
    #left and right index pointer
    l, r = 0, 0
    result = []
    while l<len(left) and r<len(right):
        if left[l] < right[r]:
            result.append(left[l])
            l += 1
        else:
            result.append(right[r])
            r += 1
    result += left[l:]
    result += right[r:]
    return result

1.2 Time complexity of merge sort

Optimal time complexity: O(nlogn)
Worst time complexity: O(nlogn)
Stability: stable

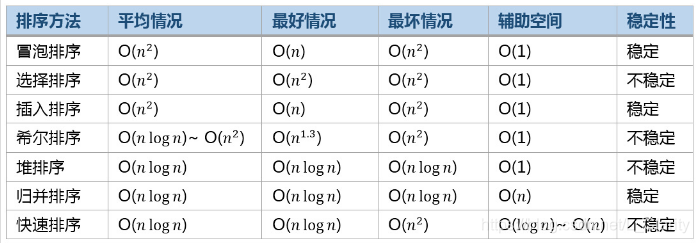
2. Comparison of the efficiency of common sorting algorithms

3. Search

Searching is the algorithmic process of finding a specific item in a collection of items. Search usually answer is true or false because of whether the item exists. Several common methods of searching: sequential search, binary search, binary tree search, hash search.

3.1 Binary search

Binary search
Advantages: fewer comparisons, fast search speed, good average performance
Disadvantages: The table to be checked is required to be an ordered table, and it is difficult to insert and delete.

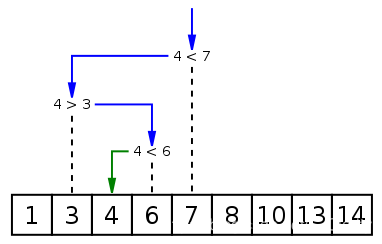
3.1.1 The realization of binary search

① Non-recursive implementation

def binary_search(alist, item):
      first = 0
      last = len(alist)-1
      while first<=last:
          midpoint = (first + last)/2
          if alist[midpoint] == item:
              return True
          elif item < alist[midpoint]:
              last = midpoint-1
          else:
              first = midpoint+1
    return False
testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,]
print(binary_search(testlist, 3))
print(binary_search(testlist, 13))

②Recursive realization

def binary_search(alist, item):
    if len(alist) == 0:
        return False
    else:
        midpoint = len(alist)//2
        if alist[midpoint]==item:
          return True
        else:
          if item<alist[midpoint]:
            return binary_search(alist[:midpoint],item)
          else:
            return binary_search(alist[midpoint+1:],item)

testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,]
print(binary_search(testlist, 3))
print(binary_search(testlist, 13))

3.1.2 Time complexity of binary search

Optimal time complexity: O(1)
Worst time complexity: O(logn)